研究生课程：机器学习-第2章 贝叶斯学习

《机器学习》课程笔记：第2章 贝叶斯学习

第2章 贝叶斯学习

概述

1. 依赖先验的决策：

某地全年365天，晴朗265天，非晴朗100天。判断明天天气如何？

令，，则：

，，因此，明天晴天的概率更大。

2. 若增加可观测信息：晴朗（非晴朗）天气前一天特征（是否有晚霞）的统计。

令，，，，，，

今天有晚霞，判断明天天气如何？ 即计算，

今天没有晚霞，判断明天天气如何？ 即计算，

利用贝叶斯决策原理：

和的联合概率：

因此可以求得，则在前一天有晚霞的条件下晴天的概率要大于不是晴天的概率。

贝叶斯决策论

贝叶斯公式：

因此

贝叶斯决策：

基于观察特征、类别的贝叶斯公式：

也就是：

因此，即

如果存在，两个变量进行决策，即计算，则可以转换为计算，

更改为比值的形式：

可以定义类别相似性函数

分母都是相同的，因此可以将转化为

概率有很多都是的形式，因此可以将转化为，将乘积的形式转换为和的形式。

对于两变量决策问题来说，可以计算决策边界，绘制后可以直观看出边界的形状，可能是直线也可能是曲线，这样实现了贝叶斯决策方法。

贝叶斯分类器

• 朴素贝叶斯分类器：假设中特征向量的各维属性独立；
• 半朴素贝叶斯分类器：假设中的各维属性存在依赖；
• 正态分布的贝叶斯分类器：假设服从正态分布；

朴素贝叶斯分类器

采用了“属性条件独立性假设”

关键问题：由训练样本学习类别条件概率和类别先验概率和

包括的个属性和的个类别，加上，共有个概率分布需要统计。

类别先验概率

类别概率密度 ，

对于来说，若是离散的变量，则 ，其中表示中在第个属性上取值为的样本组成的集合。

若是连续的变量，则 （由某一概率分布估计类别概率）

拉普拉斯平滑：避免因训练集样本不充分而导致概率估计值为零。

平滑后：，为类别数；，为的可能取值个数。

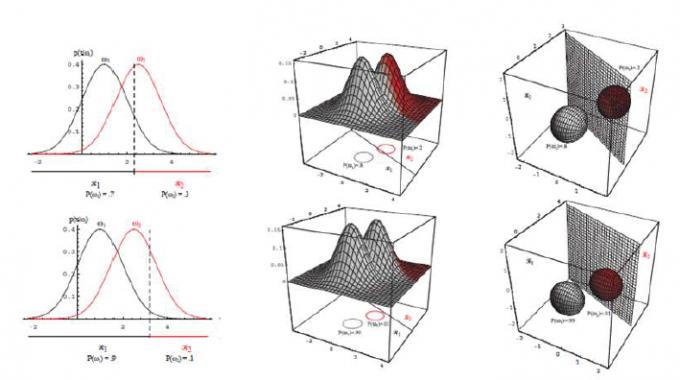
正态分布的贝叶斯分类器

若是连续的变量，则 （设置其为正态分布的概率密度）

多维正态分布的概率密度：

在每个维度上都是正态分布：

贝叶斯学习将公式化简为对数的形式：

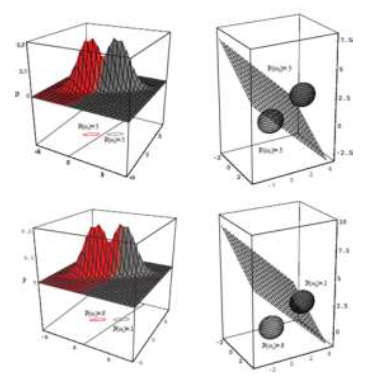
不同的高斯参数情况：

：均为正态分布（当各个类别先验相等时，退化为最小距离分类器，退化为垂直平分面）

：各类分布都相同

贝叶斯学习与参数估计问题

推导