研究生课程：高级人工智能-第2讲 搜索

《高级人工智能》课程笔记：第2讲 搜索

第2讲 搜索

搜索问题：有策略有规律的探索

搜索问题是对原问题的建模

搜索问题的构成：状态空间➡后继函数（状态转化为另一个状态，采取的动作，付出的代价）➡初始状态和目标测试

解是一个行动序列，将初始状态转换成目标状态

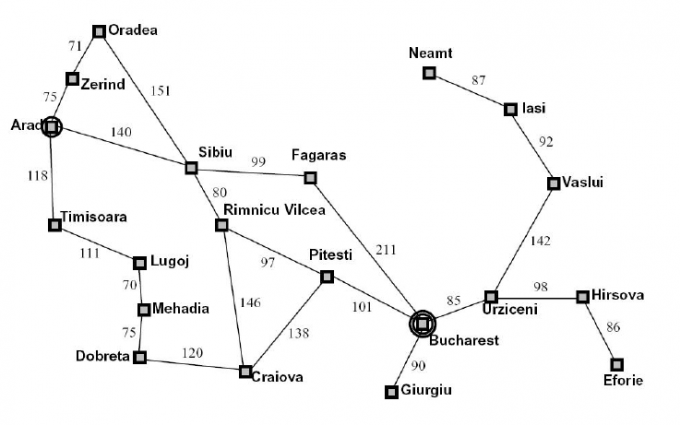
例1：罗马尼亚旅行：

• ①状态空间：所有城市
• ②后继函数：沿着道路从一个城市到达另外一个城市，损失函数是距离
• ③初始状态：这个人现在在Arad
• ④目标测试：目前是否到达了Bucharest

解：从Arad到Bucharest的最短路径

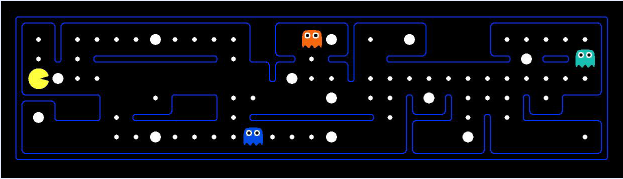
例2：吃豆子游戏

状态空间包含了环境中的每一个细节：Agent，Ghost，大的豆子和小的豆子

搜索状态只保留行动需要的细节：

对于走到终点来说：

• ①状态空间：Agent的位置信息
• ②后继函数：四个方向进行行走，更新位置信息
• ③目标测试：是否到达了终点

对于吃掉所有豆子来说：

• ①状态空间：Agent的位置信息和每一个点的状态（豆子吃没吃掉）
• ②后继函数：四个方向进行行走，更新位置信息，更新豆子的信息
• ③目标测试：全部豆子是否都被吃光

状态数量计算：

• Agent的状态：120
• 食物数量：30
• 鬼魂的位置：12*12
• 朝向：4
• 世界状态：
• 路线规划状态：120
• “吃光豆子”状态：

例3：三个传教士和三个野人

状态空间：{(M, C, B)}，表示河左岸的传教士数量、野人数量和船目前的方位

后继函数：{P01, P10, P02, P20, P11, Q01, Q10, Q02, Q20, Q11}，P表示现在是从左岸到右岸，后面两个数字表示船上的传教士数量和野人数量

初始状态：(3, 3, 1)

目标状态：(0, 0, 0)

状态空间图：搜索问题的数学表示，在状态空间图中，每个状态只出现一次

搜索树：

• 根节点对应了初始状态
• 子节点对应了父节点的后继
• 节点显示状态，但对应的是到达这些状态的行动
• 对大多数问题，实际上不会构建整个树，一般都会剪枝

状态空间图的每一个结点表示每一个状态

搜索树的每一个结点不表示状态，而是从初始状态到这个状态的一个路径（因此要尽量少构建搜索树的结点）

无信息搜索

基于搜索树的搜索：

• 扩展出潜在的行动 (tree nodes)
• 维护所考虑行动的边缘(fringe)节点
• 试图扩展尽可能少的树节点

搜索算法特性：

• 完备性: 当问题有解时，保证能找到一个解?
• 最优性: 保证能找到最优解（最小耗散路径）?
• 时间复杂度和空间复杂度？

所有搜索算法都是相同的，除了对边缘的处理策略

深度优先搜索

• 在找到目标之前，搜索到整个树左侧的一些子树
• 可以遍历整个树
• 分支因子为，最大深度为，时间复杂度为，空间复杂度为（因为只保留了路径上的结点）
• 完备性：不完备。如果无穷大，无法在可以接受的时间内找到解
• 不是最优的：只去找最左边的结点

广度优先搜索

• 在找到目标之前，搜索到全部更浅的结点
• 分支因子为，最大深度为，解的深度为，时间复杂度为，空间复杂度为
• 完备性：完备。因为如果解存在，一定是有限的
• 只有所有的路径代价都相同时才是最优的

迭代深入搜索（Iterative Deepening）

结合DFS的空间优势与BFS的时间优势

深度优先按照层数进行约束，不要搜索到层

通常绝大多数的节点都在底层，所以上层的节点生成多次影响不是很大

代价敏感搜索（Cost-Sensitive Search）

代价一致搜索(Uniform Cost Search)：将之前的走过的路径的代价进行一个累加，然后寻找其代价最低的路径。

可以看成代价敏感搜索的一种实现。

• 在找到目标之前，搜索到比代价最小的方式更小代价的结点
• 解的代价为，每条结点间连线的代价大概为，时间复杂度为，空间复杂度为
• 完备性：完备。前提是代价都是有限且都为正数。
• 最优的

启发式搜索

启发策略：估计一个状态到目标距离的函数，问题给予算法的额外信息，为特定搜索问题而设计。

贪婪搜索

策略：扩展你认为最接近目标状态的节点

启发式：对每个状态估计到最近目标的距离（曼哈顿距离或者欧氏距离），只使用启发函数来评价节点

通常情况下最佳优先使你直接（或很快）到达目标，最坏情况类似DFS

A* 搜索

结合代价一致搜索和贪婪搜索

重点搜索评价函数：

表示路径的代价，或者称为后向的代价

表示前方距离目标的距离，或者称为前向的代价

A* 搜索将两个代价进行组合

A* 搜索结束条件是目标出列的时候，而不是目标入列的时候，因为目标入列的时候可能路径并不是最优的。

A*搜索不一定是最优的，启发函数要好好选择

启发函数是可采纳的，那么，其中是到最近目标的真实耗散。（例如曼哈顿距离）

前提：启发函数是可采纳的，那么A* 树搜索是最优的。

• 代价一致搜索在所有“方向”上等可能的扩展
• A*搜索主要朝着目标扩展，而且能够保证最优性

对于解决难的搜索问题，大部分工作就是想出可采纳的启发函数。通常可采纳启发函数是松弛问题的解的耗散

A*图搜索与树搜索的区别在于图搜索不允许访问相同结点

图搜索中，如果启发函数是一致的，A* 搜索是最优的。

一致的：启发函数不仅仅要是可采纳的，同时在每一个局部的位置也要合理。

也就是：如果沿路径的节点估计耗散值单调递增，即，那么A*图搜索具备最优性。

通常，天然的可采纳启发函数是倾向于一致的，特别是从松弛问题中获得的启发函数

局部搜索

树搜索在边缘集合中保留未探索的替代路径（确保完备性）

局部搜索: 改进单一选项直到不能再改善为止

爬山法搜索

模拟退火搜索：避免局部极大（允许向山下移动）

遗传算法——自然选择

• 基于适应度函数，在每步中保留N个最好状态
• 配对杂交操作
• 产生可选的变异