研究生课程：机器学习-第3章 线性分类

《机器学习》课程笔记：第3章 线性分类

第3章 线性分类

基础知识

个数组成的有序数组, 称为一个维向量

向量空间：所有分量为实数的维向量构成的集合称为一个维向量空间，又称线性空间。

超平面表达式：

线性判别函数表达式：

线性函数刻画了样本到超平面的距离

相似性测度：

• Minkovski Metric 闵氏距离（p-范数）
• 欧氏距离（p=2）（2-范数）
• 城市块(p=1)、曼哈顿距离（1-范数）
• Chobychev 距离(p=inf)
• 平方距离\马氏距离
• 余弦相似性

常用的统计量：

• 类均值向量
• 总均值向量，
• 类内散度矩阵
• 总类内离散度矩阵
• 类间散度矩阵

分类问题

1. 定义：根据给定的训练集，其中，要求寻找上的决策函数
2. 评估方法
   1. 留出法数据集分成两类，交叉验证。
   2. 交叉验证法数据集分成类，其中类做测试，类做训练；进行次实验取平均。
   3. 自助法次随机取一个样本, 共个样本，放入中；由训练，测试。
3. 性能评价
   1. 错误率与精度：，
   2. 查准率、查全率与F1
   3. ROC 与AUC
   4. 代价敏感错误率与代价曲线
4. 比较检验
   1. 假设检验
   2. 交叉验证检验
   3. McNemar检验
   4. Friedman检验与Nemenyi检验

线性分类问题

1. 线性分类器描述：
   1. 线性判别函数：
   2. 分类界为超平面：
2. 线性分类器的任务：通过已知的训练样本集, 构造线性判别函数
3. 线性可分性

线性决策的多分类问题：

类问题，需要至少预先训练多少个二分类器？

需要训练好个分类器（所有可能的分类器），然后采用二叉树比对测试。

根据最大相似性决定类别。

感知机

基本知识：

1. 神经网络形成阶段（1943-1958），开拓性的贡献
2. 线性分类：
   1. 决策函数：
   2. 增广表示：，其中
   3. 决策超平面：
   4. 分类判别：根据是否大于0进行判断
   5. 决策函数几何含义：刻画了样本到超平面的距离
   6. 验证函数：
3. 优化方法：梯度下降
   1. 随机梯度下降：

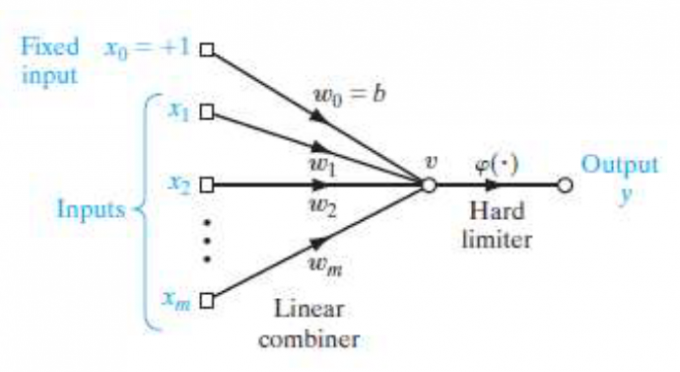
感知机结构

感知机学习准则：目标：最小化错分样本的误差代价。

代价函数（错分样本的误差函数）：（只统计错分的样本，是错分的样本到超平面的距离之和）

的含义：错分样本到分类超平面误差距离的总和

感知机优化：Batch Perception和Online Perception

误差修正基本规则：

1. 固定增量的感知机修正：若训练样本是线性可分，则感知器训练算法在有限次迭代后可以收敛到正确的解向量。
2. 增量自适应调整：当错分样本的正确标签为，修正；当错分样本的正确标签为，修正

线性鉴别分析

基本思想：求线性变换，使得样本集${x_i} {y_i} $后，类别间距大，类内间距小。

目标函数：（）

样本投影后的类别间距离： ； 其中， 表示第 类样本投影后的均值

样本投影后的类别内距离：投影后的各类样本方差

计算：

logistic 模型

基本思想：假设likelihood ratio的对数为线性判别函数

两类问题：

，

学习目标：

标签 类, 越大, 越小，标签 类, 越大, 越小。