《模式识别与机器学习》课程笔记：第4章 特征选择和提取

第4章 特征选择和提取

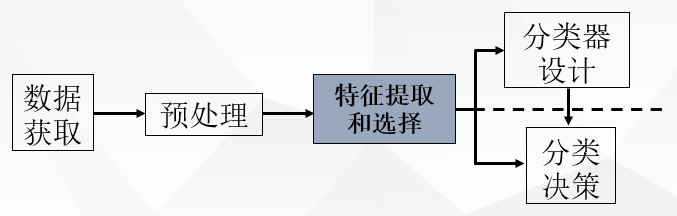
特征选择和提取是模式识别中的一个关键问题，前面讨论分类器设计的时候，一直假定已给出了特征向量维数确定的样本集，其中各样本的每一维都是该样本的一个特征；这些特征的选择是很重要的，它强烈地影响到分类器的设计及其性能；假若对不同的类别，这些特征的差别很大，则比较容易设计出具有较好性能的分类器。

例如，描述人可以用好多特征，如肤色，体重，身高等，但是如果要判断软件工程师，显然编程这个特征比较有判别性；如果要判断是不是篮球员，则体重、身高有很强的判别性。

特征选择和提取是构造模式识别系统时的一个重要课题。在很多实际问题中，往往不容易找到那些最重要的特征，或受客观条件的限制，不能对它们进行有效的测量；因此在测量时，由于人们心理上的作用，只要条件许可总希望把特征取得多一些；另外，由于客观上的需要，为了突出某些有用信息，抑制无用信息，有意加上一些比值、指数或对数等组合计算特征；如果将数目很多的测量值不做分析，全部直接用作分类特征，不但耗时，而且会影响到分类的效果，产生“特征维数灾难”问题。

为了设计出效果好的分类器，通常需要对原始的测量值集合进行分析，经过选择或变换处理，组成有效的识别特征；在保证一定分类精度的前提下，减少特征维数，即进行“降维”处理，使分类器实现快速、准确和高效的分类。为达到上述目的，关键是所提供的识别特征应具有很好的可分性，使分类器容易判别。为此，需对特征进行选择：

• 应去掉模棱两可、不易判别的特征；
• 所提供的特征不要重复，即去掉那些相关性强且没有增加更多分类信息的特征。

特征选择和提取这一任务应在设计分类器之前进行；

所谓特征选择，就是从个度量值集合中，按某一准则选取出供分类用的子集，作为降维（维，）的分类特征；

所谓特征提取，就是使通过某种变换，产生个特征 ，作为新的分类特征（或称为二次特征）；

其目的都是为了在尽可能保留识别信息的前提下，降低特征空间的维数，以达到有效的分类效果。

模式类别可分性的测度

距离和散布矩阵：

• 点到点之间的距离：，其中, 和 为 维向量, 其第 个分量分别是 和
• 点到点集之间的距离：点到点集之间的距离为

类内距离：维空间中同一类内各模式样本点集，其内部各点的均方距离为，其中

类内散布矩阵：考虑一类内模式点集，其类内散布矩阵为：，其中

对属于同一类的模式样本，类内散布矩阵表示各样本点围绕其均值周围的散布情况。

在考虑有两个以上的类别，如集合时，类间距离对类别的可分性起着重要作用，此时应计算

为简化起见，常用两类样本各自质心间的距离作为类间距离，并假设两类样本出现的概率相等，则

其中和为两类模式样本集各自的均值向量， 和 为和的第个分量，为维数。

两类模式的类间散布矩阵：

对三个以上的类别，类间散布矩阵常写成，其中，为多类模式（如共有类）分布的总体均值向量，即

多类情况的类内散布矩阵可写成各类的类内散布矩阵的先验概率的加权和，即，其中是第类的协方差矩阵。

有时，用多类模式总体分布的散布矩阵来反映其可分性，即：，其中为多类模式分布的总体均值向量。

，即总体散布矩阵是各类类内散布矩阵与类间散布矩阵之和。

特征选择

设有个可用作分类的测量值，为了在不降低（或尽量不降低）分类精度的前提下，减小特征空间的维数以减少计算量，需从中直接选出个作为分类的特征。

从个测量值中选出个特征，一共有种可能的选法，需寻找一种简便的可分性准则，间接判断每一种子集的优劣。

对于独立特征的选择准则：类别可分性准则应具有这样的特点，即不同类别模式特征的均值向量之间的距离应最大，而属于同一类的模式特征，其方差之和应最小。假设各原始特征测量值是统计独立的，此时，只需对训练样本的个测量值独立地进行分析，从中选出个最好的作为分类特征即可。

对于 和 两类训练样本，假设其均值向量为 和 ，维方向的分量为 和 ，方差为 和 ，定义可分性准则函数，则为正值。 值越大，表示测度值的第个分量对分离 和 类越有效。将按大小排队, 选出最大的个对应测度值作为分类特征，即达到特征选择的目的。

上述基于距离测度的可分性准则，其适用范围与模式特征的分布有关。假若类概率密度函数不是或不近似正态分布，均值和方差就不足以用来估计类别的可分性，此时该准则函数不完全适用。

一般特征的散布矩阵准则：

• 类内：
• 类间：

直观上，类间离散度越大且类内离散度越小，则可分性越好。因此，可推导出散布矩阵准则采用如下形式：

• 行列式形式：
• 迹形式：

其中， 是矩阵 的特征值。使 或 最大的子集可作为选择的分类特征。

离散K-L变换（Karhunen-Loeve变换（卡洛南-洛伊变换））

前面讨论的特征选择是在一定准则下，从个特征中选出个来反映原有模式。这种简单删掉某个特征的做法并不十分理想，因为一般来说，原来的个数据各自在不同程度上反映了识别对象的某些特征，简单地删去某些特征可能会丢失较多的有用信息。如果将原来的特征做正交变换，获得的每个数据都是原来个数据的线性组合，然后从新的数据中选出少数几个，使其尽可能多地反映各类模式之间的差异，而这些特征间又尽可能相互独立，则比单纯的选择方法更灵活、更有效。

K-L变换就是一种适用于任意概率密度函数的正交变换。

离散的有限K-L展开

离散的有限K-L展开式的形式：

设一连续的随机实函数，则 可用已知的正交函数集 的线性组合来展开，即：。式中，为展开式的随机系数，为一连续的正交函数，它应满足：,其中为的共轭复数式。

将上式写成离散的正交函数形式，使连续随机函数和连续正交函数在区间内被等间隔采样为个离散点，即：

，

写成向量形式：，

将展开式写成离散形式：，其中为展开式中随机系数的向量形式，为维矩阵，其中，每一列为正交函数集中的一个函数，小括号内的序号为正交函数的采样点次序。因此，实质上是由向量组成的正交变换矩阵，
它将变换成。

对各个模式类别，正交函数都是相同的，但其展开系数向量则因类别的不同模式分布而异。

K-L展开式的根本性质是将随机向量展开为另一组正交向量的线性和，且其展开式系数（即系数向量的各个分量）具有不同的性质。

正交向量集的确定：

设随机向量的总体自相关矩阵为，则，要求系数向量的各个不同分量应统计独立，则应使，其中为对角形矩阵，其互相关成分均为0

因为是实对称矩阵，其不同特征值对应的特征向量应正交，即：

K-L展开式系数的计算步骤：

1. 求随机向量的自相关矩阵：
2. 求出矩阵的特征值和对应的特征向量，，得矩阵：
3. 计算展开式系数：

按K-L展开式选择特征

K-L展开式用于特征选择相当于一种线性变换。若从个特征向量中取出个组成变换矩阵，即，此时是一个维矩阵，是维向量，经过变换，即得到降维为的新向量。

结论

从K-L展开式的性质和按最小均方差的准则来选择特征，应使。由于，故应使。基于这一条件，在将整体模式进行K-L变换之前，应先将其均值作为新坐标轴的原点，采用协方差矩阵或自相关矩阵来计算特征值。如果，则只能得到“次最佳”的结果。

将K-L展开式系数（亦即变换后的特征）用表示，写成向量形式：，此时变换矩阵用个特征向量组成。为使误差最小，不采用的特征向量，其对应的特征值应尽可能小。因此，将特征值按大小次序标号，即。若首先采用前面的个特征向量，便可使变换误差最小。此时的变换矩阵为，

K-L变换是在均方误差最小的意义下获得数据压缩（降维）的最佳变换，且不受模式分布的限制。对于一种类别的模式特征提取，它不存在特征分类问题，只是实现用低维的个特征来表示原来高维的个特征，使其误差最小，亦即使其整个模式分布结构尽可能保持不变。

通过K-L变换能获得互不相关的新特征。若采用较大特征值对应的特征向量组成变换矩阵，则能对应地保留原模式中方差最大的特征成分，所以K-L变换起到了减小相关性、突出差异性的效果。在此情况下，K-L变换也称为主成分变换（PCA变换）。

需要指出的是，采用K-L变换作为模式分类的特征提取时，要特别注意保留不同类别的模式分类鉴别信息，仅单纯考虑尽可能代表原来模式的主成分，有时并不一定有利于分类的鉴别。