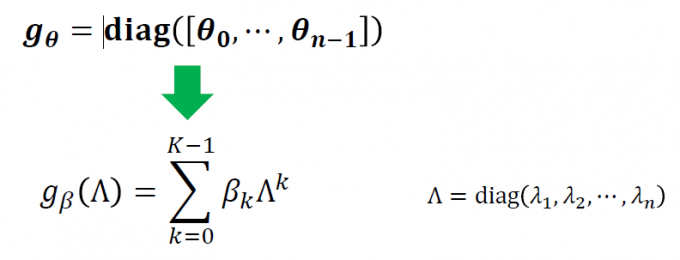研究生课程：高级人工智能-第7讲 图卷积神经网络

《高级人工智能》课程笔记：第7讲 图卷积神经网络

第7讲 图卷积神经网络

卷积神经网络在欧式数据（图像、文本、声音和视频等）上获得了巨大的成功，广泛应用于图像分类、目标检测、机器翻译等

卷积神经网络可以学习局部小结构，使用局部的卷积核，然后形成多维的模式

卷积如何迁移到非欧空间上去？

卷积是在函数和函数上的数学运算，从而得到函数

连续形式：

离散形式：

在图上定义卷积的方法：

谱方法：在谱空间中定义卷积：

• 通过图傅里叶变换和卷积原理定义卷积
  • 图数据符合幂律分布，造成了极大的挑战
• 主要挑战是在谱空间定义的卷积在结点空间并没有局部化

空间方法：在向量空间中定义卷积

• 卷积被定义为目标结点到它的所有邻居的一个加权平均函数
• 主要挑战是邻域的大小在结点之间差异很大，可能服从幂律分布

谱方法

定义一个图（结点、边、邻接矩阵）

图上的每个结点上都有维的特征，因此是结点的特征矩阵，每一列是结点的一个信号

图的拉普拉斯算子：，其中

归一化的拉普拉斯算子：

图的傅里叶变换：

的正交特征向量是，对应的非负特征值是，可以对拉普拉斯矩阵进行分解：

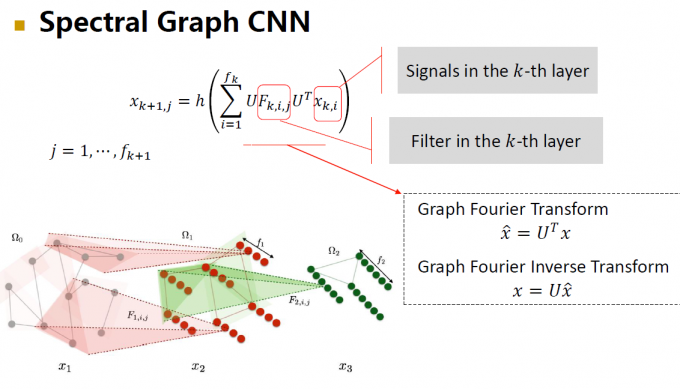
对于一个信号的图傅里叶变换为

两个信号的卷积的傅里叶变换是两个信号的傅里叶变换的逐点相乘，卷积核就是

图卷积神经网络：

缺点：

• 需要拉普拉斯矩阵的特征分解，特征向量不太好获得
• 计算成本高，傅里叶乘法的时间复杂度是
• 在结点空间上不是局部化的（操作的是全局信号）

ChebyNet：参数化-将参数的数量从n降为K

优点：

• 不再需要特征分解
• 时间复杂度从下降到
• 卷积在结点空间上是局部化的（卷积严格定位在半径为 K 的球中）

Graph wavelet neural network：图小波神经网络

将傅里叶基换为小波基：稀疏、局部化、计算代价低

空间方法

方法类比卷积：

1. 对于每个节点，根据某些邻近度指标选择固定数量的结点作为其相邻结点
2. 根据邻近度指标给邻居排序
3. 共享参数

GraphSAGE：从每个结点开始随机游走，采样个结点，不用临近度指标判断。然后通过聚合函数进行参数共享

图卷积网络（GCN）：通过归一化的拉普拉斯矩阵从不固定数量的邻居结点中聚合信息，通过特征变换共享参数

GAT：Graph Attention Network：通过注意力机制学习聚合矩阵

MoNet：空间方法的一般意义框架：所有的空间方法都是定义多个核函数，来测量目标结点和其他结点之间的相似度

谱方法与空间方法的关系

谱方法是空间方法的特例

• 谱方法通过特别的空间变换定义核函数
• 空间方法直接定义核函数

图池化

图粗化：将结点进行聚类，每一类作为一个超级结点

结点选择：学习一个评价标准去挑选比较重要的结点

图神经网络的表达能力

图神经网络在结点分类、链接预测、图分类上取得了巨大的成功，但是图神经网络的设计大多基于直觉、启发式方法或者实验试错，缺少对于图神经网络的理论理解。