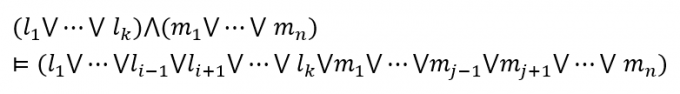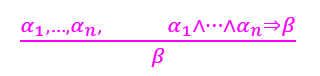《高级人工智能》课程笔记：第8讲 逻辑

第8讲 逻辑

什么是“数理逻辑”？

• 一种“算法”：输入+输出，不仅要得到算法，还要证明是正确的
• 一种“关于证明、推理等思考活动”的算法

一个算法，以任何作为输入，输出的都是正确答案

输入：

• 知识库：任意的问题假设，前提条件等
• 查询：想要解决的问题

输出答案：该查询在此知识库上的正确答案

如果有上面的算法，那么所有难题都能得到解决

如果有这样的一种“终极算法”，首先要将自然语言表达的知识库和查询表示成形式语言表达的知识库和查询，然后通过自动的知识推理，得到形式语言表达的答案

逻辑的研究内容

解决如下问题：

• 关于逻辑的形式语言是什么
• 在形式语言上的自动推理的算法是什么
  • 该算法复杂度如何，是否可以更高效
• 自动推理的算法是否正确
  • 算法正确性的严格证明

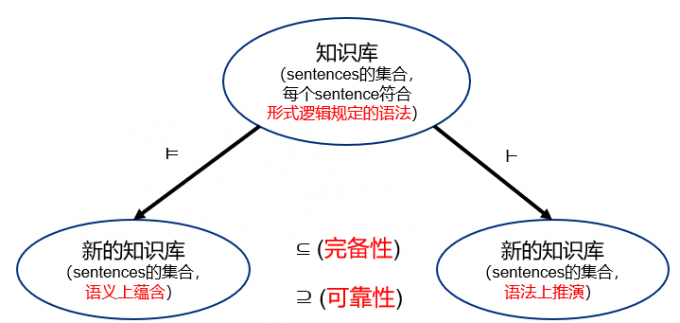
研究形式化定义的sentences之间的关系

左侧是语义的蕴含关系（逻辑推导），，从知识库出发一定正确的知识

右侧是语法的演绎关系（形式推演），，通过算法可以从知识库推出的

如果左侧的是右侧的子集，说明正确的结论都在算法推导的里面，那么说明这个算法是完备的，但是有一些结论可能算法计算出来是错误的

如果右侧的是左侧的子集，说明算法推出来的结论都是正确的，因此算法是可靠的，但是有可能有一些正确的结论算法算不出来

如果兼具完备性和可靠性，那么证明这个算法是正确的。

语义

如果在的条件下是 true，那么称是句子的一个 model，句子的所有model的集合是

KB指的是一些句子的集合

：在任意的条件下（一个真值指派）只要成立，一定成立，称为 KB蕴含

因此与完全等价（当且仅当）（，是不可满足的）

命题逻辑

语法（逻辑推导）

命题是一种声明，要么是真的，要么是假的，不存在第三种可能

命题逻辑通常不考虑时间

原子命题指的是最小的命题，用大写字母表达

文字是原子命题，或者是原子命题的否

一个句子是一个原子句或者复杂句

一个原子句表示为：

复杂句有五种表示形式，与复杂句之间的真值表：

false	false	true	false	false	true	true
false	true	true	false	true	true	false
true	false	false	false	true	false	false
true	true	false	true	true	true	true

连接词和集合之间的联系：

两个句子是逻辑等价的-两个句子的model相同： 当且仅当 且

定理：

KB: 满足命题逻辑语法的sentence的集合

假设：这组sentence中，一共有n个原子命题

真值指派（truth assignment）：对每个原子名字赋值

一共有种真值指派，其中：使得KB中的每个sentence都为真的真值指派，就是KB的model

在此基础上，在命题逻辑中，我们可以明确的定义

• 如果一个句子在任意的model下面都为true，则这个句子是永真的
• 演绎定理： 当且仅当是永真的
• 如果一个句子在某些model下为真，则称这个句子是可满足的
• 如果一个句子在任何model下都为假，则称这个句子是不可满足的
• 当且仅当是不可满足的

蕴含，不是连接词：描述的是蕴含的一种关系，有了知识表示后，额外推出其他的知识

命题逻辑里面的连接词，用于知识表示（实际上是可以替代的，但是引入这个符号进行知识表示比较方便）

形式推演

推出：，通过算法可以从知识库推出的

共有两套规则（11条规则和归结原理）

11条形式推演规则：（不需要背诵）

形式可推演性：A在命题逻辑中由形式可推演的，记作，当且仅当能由（有限次使用）命题逻辑的形式推演规则生成

句子可以通过规则从KB中得出，记作

可靠性：任意时刻当时，同时成立，那么说是可靠的

完备性：任意时刻当时，同时成立，那么说是完备的

归结原理

合取范式：子句（文字和析取符号）的合取形式，子句内部是没有合取的（CNF）转换为合取范式是多项式时间复杂度的

归结原理：互补文字可以互相消去（但是每一次只能消去一对）

归结原理是既可靠又完备的

证明：若，当且仅当，其中仅使用归结法则获得新子句

使用上述证明来证明知识库可以推出某个子句

证明：归结原理既可靠又完备

在研究可靠性与完备性问题时，应当把语法层面的知识理解为Groundtruth

因此可靠性可以大概表述为：语义上推演得到的知识在语法上正确。因此要证明归结原理的可靠性，即证明

使用真值表进行证明即可

完备性可以大概表述为：如果语法上能够推理得到的，那么语义上正确。

即证明：如果，则

RC(S)：对S内部的全部子句进行归结后的集合。

完备性证明

等价于永假，等价于是不可满足的。

等价于可以归结出空子句，即RC(S)包含空子句

则只需要证明：如果是不可满足的，则RC(S)包含空子句

等价于证明逆否命题：如果RC(S)不包含空子句，则是可满足的

证明：针对S中的原子命题，我们构造如下的model：

首先，因为RC(S)中不包含空集，即RC(S)中不包含永假的子句。

从到 , 顺序指派的真值：

如果RC(S)中包含一个子句，此子句包含，且此子句的其它文字都已经被指派为False（在之前的步骤中进行的）或不包含其它文字，则把指派为False；否则，把指派为True

我们用反证法证明：这个真值指派使得RC(S)中的子句都为真。

假设，在此过程的第i步，我们这样来指派使得某个子句C为False，且假设这是首次出现False的子句；此时，子句C只能是如下两种形式之一：或者

显然，如果RC(S)中只包含以上两个子句之一，子句C是不会在此真值指派中为False的。因此， RC(S)此时应该同时包含了以上两个子句。

以上两个子句显然是满足归结条件的，也就是说，它归结后的子句也应该在RC(S)中；同时，该子句已经被指派为False了；这与我们之前的假设矛盾。

因此这个真值指派使得RC(S)中的子句都为真，进而S是可满足的。

可以转换为搜索问题，如何使用A*搜索实现呢？

Modus Ponens规则

以限制知识库里面的句子形式为代价，获得时间复杂度上的提升

上述提到的归结原理具有完备性，这是很好的性质，对于许多现实世界的应用，如果添加一些限制，可以实现更高效的推理。为了换取更好的inference的时间效率，缩小命题逻辑的表达范围，得到适用于Horn Form的Modus Ponens规则，是另外一种形式的归结原理。

KB为Definite clause的合取形式：

Definite clause: 每一个句子有且只有一个文字是正文字的析取形式

只有两种形式：①原子命题②命题的合取另外一个命题

Horn clause: 每一个句子最多一个文字是正文字的析取形式

PPT例子：KB是全部句子的情况下是否能推出Q

前向推理：从条件出发去推结论

前向推理是数据驱动的，可能推出一些结论与我们要推出的结论是无关的

后向推理：从结论返回推出条件

后向推理是目的驱动的，找为了推出这个结论所需要的条件，因此通常情况下后向推理比前向推理好，但是也存在某种情况前向推理比后向推理好

（全连接神经网络）

Modus Ponens规则证明

证明是可靠的，即证明

通过真值表进行证明即可

证明是完备的：

若，。此时，中仅包含definite子句，仅使用Modus Ponens规则，且是一个正文字

证明：RC(KB)是KB中原始的句子和通过Modus Ponens推出的句子的全部集合

1. 构造如下的真值指派：对于任意的symbol a，a指派为True当且仅当

（如果一个正文字在中，就设为True，不在就设置为False）

2. 接下来证明：在下，为真。

反证：若此时为False，那么：必存在一个definite子句，在下为False。

若该子句为 也就是说，在m中，均为True，且为False。根据1中的定义， ，又根据Modus Ponens规则，根据1中的定义，在中， 为True。推出矛盾。

若该子句为，在下为为False，则，矛盾

3. 若，根据蕴含的定义：在中，为真；则根据1中的定义，，也就是说：

命题逻辑的缺点：能表达的东西比较有限。

一阶谓词逻辑

语法和语义

命题逻辑假设世界上都是事实(fact)，一阶谓词逻辑认为世界上还包括对象、关系和函数等等。

基本元素：

1. 常量和变量
2. 谓词（哥哥、大于等）Predicates
3. 函数
4. 连接词（与命题逻辑的连接词完全相同）
5. ，为真当且仅当和指向现实世界中的同一个对象
6. 量词：全称量词和存在量词

简单句与复杂句

简单句：或

或常量或变量

嵌套函数会造成很大的问题。命题逻辑的算法一定会停止(decidable可判定的)，但是由于嵌套函数的存在，谓词逻辑只是半可判定的。

复杂句：使用连接词对简单句进行连接构成复杂句

量词

在谓词逻辑中，要将每一个符号指派到现实世界中，将常量转化为对象、将谓词转化为关系、将函数符号转化为真正的函数

量词与变量是对应的，有变量一定要有量词来量化

全称量词：变量所有实例的合取形式

错误的形式：

存在量词：变量所有实例的析取形式

错误的形式：

量词的属性关系

两种量词之间可以相互转换

一阶谓词的形式推演（命题化）

全称实例化：实例化全称量词蕴含的每一个实例

注意在实例化的过程中，第n次循环只能嵌套n次函数

因此算法可能不会停止，为semi-decidable的

存在实例化：赋予一个新的常量符号

一阶谓词逻辑的归结原理

去掉存在量词和存在量词修饰的变量，使得句子里面的每一个变量都是全称量词修饰的变量，且为合取范式

合一算子：替换后等价的替换方式（只能将常量赋值给变量）

归结原理：

尤其注意要赋值

归结原理既完备又可靠，证明比较复杂不讲

归结策略

可能有很多的归结策略，选择哪种方式进行归结呢？

没有一种归结策略适用于全部情况

广度优先策略：扩展所有可能的情况然后归结

优点：

• 当问题有解时保证能找到最短归结路径。
• 是一种完备的归结策略。

缺点：

• 归结出了许多无用的子句
• 既浪费时间，又浪费空间

广度优先对大问题的归结容易产生组合爆炸，但对小问题却仍是一种比较好的归结策略。

常用的归结策略可分为两大类：

• 删除策略是通过删除某些无用的子句来缩小归结范围
• 限制策略是通过对参加归结的子句进行某些限制，来减少归结的盲目性，以尽快得到空子句。

删除策略

删除法主要想法是：把子句集中无用的子句删除掉，这就会缩小搜索范围，减少比较次数，从而提高归结效率。

删除纯文字：

• 如果某文字在子句集中不存在可与其互补的文字，则称该文字为纯文字。
• 在归结过程中，纯文字不可能被消除，用包含纯文字的子句进行归结也不可能得到空子句
• 对子句集而言，删除包含纯文字的子句，是不影响其不可满足性的。

重言式删除法：

• 如果一个子句中包含有互补的文字对，则称该子句为重言式。
• 重言式是真值为真的子句。对一个子句集来说，不管是增加还是删除一个真值为真的子句，都不会影响该子句集的不可满足性。
• 因此，可从子句集中删去重言式。

限制策略

限制策略要慎重，防止可以得到空子句但是限制后就得不到空子句了

支持集策略：每一次参加归结的两个亲本子句中，至少应该有一个是由目标公式的否定所得到的子句或它们的后裔。（就是别自己本身进行归结，带上一起归结）

支持集策略是完备的，即当子句集为不可满足时，则由支持集策略一定能够归结出一个空子句。

• 可以把支持集策略看成是在广度优先策略中引入了某种限制条件，这种限制条件代表一种启发信息，因而有较高的效率
• 支持集策略限制了子句集元素的剧增，但会增加空子句所在的深度（结果可能不是最优）。
• 支持集策略具有逆向推理的含义，由于进行归结的亲本子句中至少有一个与目标子句有关，因此推理过程可以看作是沿目标、子目标的方向前进的。

单文字子句策略：每次参加归结的两个亲本子句中至少有一个子句是单文字子句

采用单文字子句策略，归结式包含的文字数将少于其非单文字亲本子句中的文字数，这将有利于向空子句的方向发展，因此会有较高的归结效率。

单文字子句策略是不完备的，即当子句集为不可满足时，用这种策略不一定能归结出空子句。原因： 没有可用的单文字字句

祖先过滤策略：满足以下两个条件中的任意一个就可进行归结：

• 两个亲本子句中至少有一个是初始子句集中的子句。
• 如果两个亲本子句都不是初始子句集中的子句，则一个子句应该是另一个子句的先辈子句。

祖先过滤策略是完备的

Generalized Modus Ponens（前见推理）

GMP的可靠性证明：将量词去掉变量替换为，使用命题逻辑的Modus Ponens证明即可

同样有前向推理和后向推理，同样是半可判定的

但是，如果仅包含一阶谓词的definite子句且没有函数，那么是decidable的（也叫Datalog）

模糊计算

清晰的概念：对象是否属于这个概念是明确的。

模糊性的概念：对象从属的界限是模糊的，随判断人的思维而定

取得精确数据不可能或很困难，也没有必要获取精确数据

要使计算机能够模仿人脑，对复杂系统进行识别和判断，出路何在？

1965年扎德(Zadeh)教授开创了对“模糊数学”的研究。他认为数学是可以模糊的，主张从精度方面“后退”一步。他提出用隶属函数使模糊概念数学化。

模糊集的定义

设是给定论域，是把任意映射为上某个实值的函数，即，则称为定义在上的一个隶属函数，由（对所有）所构成的集合称为上的一个模糊集，称为对的隶属度。

模糊集完全是由隶属函数来刻画的，把中的每一个元素都映射为上的一个值

的值表示隶属于的程度，其值越大，表示隶属于的程度越高。当仅取和时，模糊集便退化为一个普通集合。

模糊性：事件发生的程度，而不是一个事件是否发生

随机性：描述事件发生的不确定性，即一个事件发生与否

模糊集的表示

离散且为有限论域的表示方法

设论域为离散论域，则其模糊集可表示为：

为了能够表示出论域中的元素与其隶属度之间的对应关系，扎德引入了一种模糊集的表示方式：先为论域中的每个元素都标上其隶属度，然后再用“+”号把它们连接起来，即，其中为对的隶属度；“”不是相除关系，只是一个记号；“+”也不是算术意义上的加，只是一个连接符号。

连续论域的表示方法：如果论域是连续的，则其模糊集可用一个实函数来表示。

模糊集的运算

设分别是上的两个模糊集，对任意，都有成立，则称等于，记为

设分别是上的两个模糊集，对任意，都有成立，则称包含，记为

设分别是上的两个模糊集，则、分别称为与的并集、交集，它们的隶属函数分别为：

设为上的模糊集，称为的补集，其隶属函数为：

两个模糊集之间的运算实际上就是逐点对隶属函数作相应的运算

模糊关系

经典集合的关系：

笛卡尔积：设与是两个普通集合，与的笛卡尔乘积为

从到的关系：上的一个子集，即，记为

对于中的元素，若，则称与有关系；若，则称与没有关系

模糊集合的关系：在二元关系上定义隶属度函数

设是上的模糊集，则称

为的笛卡尔乘积，它是上的一个模糊集

在上的一个元模糊关系是指以为论域的一个模糊集，记为

设与分别是与上的两个模糊关系，则与的合成是从到的一个模糊关系，记为。其隶属函数为，其中其中，和分别表示取最小和取最大

模糊逻辑

模糊逻辑：定义模糊谓词、模糊量词、模糊修饰语等

模糊谓词：设，为模糊谓词，即U中的一个模糊关系，则模糊命题可表示为，其中的模糊谓词可以是大、小、年轻、年老、冷、暖、长、短等。

模糊量词：模糊逻辑中使用的模糊量词，如极少、很少、几个、少数、多数、大多数、几乎所有等。

模糊修饰语：

设是模糊修饰语，是变量，是模糊谓词，则模糊命题可表示为为，模糊修饰语也称为程度词，常用的程度词有“很”、“非常”、“有些”、“绝对”等。

模糊修饰语的四种主要运算：

1. 求补：表示否定，如“不”、“非”等，其隶属函数的表示为：
2. 集中：表示“很”、“非常”等，其效果是减少隶属函数的值：
3. 扩张：表示“有些”、“稍微”等，其效果是增加隶属函数的值：
4. 加强对比：表示“明确”、“确定”等，其效果是增加0.5以上隶属函数的值，减少0.5以下隶属函数的值：

演化计算

演化计算（Evolutionary Computation, EC）：

• 在基因和种群层次上模拟自然界生物进化过程与机制的问题求解技术和计算模型。
• 思想源于生物遗传学和适者生存的自然规律
• 基于达尔文（Darwin）的进化论和孟德尔（Mendel）的遗传变异理论
  • 达尔文的自然选择学说是一种被人们广泛接受的生物进化学说：
    • 生物要生存下去，就必须进行生存斗争。
    • 具有有利变异的个体容易存活下来，并且有更多的机会将有利变异传给后代；具有不利变异的个体就容易被淘汰，产生后代的机会也少的多。
    • 适者生存，不适者淘汰：自然选择。
    • 遗传和变异是决定生物进化的内在因素。（相对稳定+新的物种）

典型代表：

• 遗传算法（Genetic Algorithm, GA）
• 进化策略（Evolutionary Strategy, ES）
• 进化规划（Evolutionary Programming, EP）
• 遗传规划（Genetic Programming, GP）

演化计算：一种模拟自然界生物进化过程与机制进行问题求解的自组织、自适应的随机搜索技术。

演化规则：“物竞天择、适者生存”

演化操作：繁殖（Reproduction）、变异（Mutation）、竞争（Competition）、选择（Selection）

遗传算法

遗传算法的基本思想是从初始种群出发，采用优胜劣汰、适者生存的自然法则选择个体，并通过杂交、变异来产生新一代种群，如此逐代进化，直到满足目标为止

基本概念：

• 种群（Population）：多个备选解的集合。
• 个体（Individual）：种群中的单个元素，通常由一个用于描述其基本遗传结构的数据结构来表示。例如，长度为L的0、1串。
• 适应度（Fitness）函数：用来对种群中各个个体的环境适应性进行度量的函数，函数值是遗传算法实现优胜劣汰的主要依据
• 遗传操作（Genetic Operator）：作用于种群而产生新的种群的操作。选择（Selection）、交叉（Cross-over）、变异（Mutation）

遗传算法主要由染色体编码、初始种群设定、适应度函数设定、遗传操作设计等几大部分所组成，

算法基本步骤：

1. 选择编码策略，将问题搜索空间中每个可能的点用相应的编码策略表示出来，即形成染色体；
2. 定义遗传策略，包括种群规模N，交叉、变异方法，以及选择概率Pr、交叉概率Pc、变异概率Pm等遗传参数；
3. 令t=0，随机选择N个染色体初始化种群P(0)；
4. 定义适应度函数f；
5. 计算P(t)中每个染色体的适应值；
6. t=t+1；
7. 运用选择算子，从P(t-1)中得到P(t)；
8. 对P(t)中的每个染色体，按概率Pc参与交叉；
9. 对染色体中的基因，以概率Pm参与变异运算；
10. 判断群体性能是否满足预先设定的终止标准，若不满足返回(5)。

遗传编码

二进制编码

二进制编码是将原问题的结构变换为染色体的位串结构。假设某一参数的取值范围是。用长度为的二进制编码串来表示该参数，将等分成个子部分，记每一个等分的长度为

优点：易于理解和实现，可表示的模式数最多

缺点：海明悬崖。当算法从7改进到8时，就必须改变所有的位

格雷编码

要求两个连续整数的编码之间只能有一个码位不同，其余码位都是完全相同的。有效地解决了海明悬崖问题。

基本原理：

• 二进制码->格雷码（编码）：从最右边一位起，依次将每一位与左边一位异或，作为对应格雷码该位的值，最左边一位不变；
• 格雷码->二进制码（解码）：从左边第二位起，将每位与左边一位解码后的值异或，作为该位解码后的值，最左边一位依然不变。

符号编码

个体染色体编码串中的基因值取自一个无数值含义，而只有代码含义的符号集。

适应度函数

适应度函数是一个用于对个体的适应性进行度量的函数。个体的适应度值越大，它被遗传到下一代种群中的概率越大

常用的适应度函数

• 原始适应度函数：直接将待求解问题的目标函数定义为遗传算法的适应度函数。
  • 例如：求最大值时，即为的原始适应度函数。
  • 优点：能够直接反映出待求解问题的最初求解目标
  • 缺点：有可能出现适应度值为负的情况
• 标准适应度函数
  • 在遗传算法中，一般要求适应度函数非负，并其适应度值越大越好。这就往往需要对原始适应函数进行某种变换，将其转换为标准的度量方式，以满足进化操作的要求，这样所得到的适应度函数被称为标准适应度函数

基本遗传操作

选择(selection)操作：根据选择概率按某种策略从当前种群中挑选出一定数目的个体，使它们能够有更多的机会被遗传到下一代中

• 比例选择：各个个体被选中的概率与其适应度大小成正比。
• 轮盘赌选择：个体被选中的概率取决于该个体的相对适应度。，其中，是个体的相对适应度，即个体被选中的概率，是个体的原始适应度。

交叉(crossover)操作：按照某种方式对选择的父代个体的染色体的部分基因进行交配重组，从而形成新的个体。

二进制交叉：二进制编码情况下所采用的交叉操作

• 单点交叉：先在两个父代个体的编码串中随机设定一个交叉点，然后对这两个父代个体交叉点前面或后面部分的基因进行交换，并生成子代中的两个新的个体。
• 两点交叉：先在两个父代个体的编码串中随机设定两个交叉点，然后再按这两个交叉点进行部分基因交换，生成子代中的两个新的个体。
• 均匀交叉：先随机生成一个与父串具有相同长度的二进制串（交叉模版），然后再利用该模版对两个父串进行交叉，即将模版中1对应的位进行交换，而0对应的位不交换，依此生成子代中的两个新的个体。

实值交叉：在实数编码情况下所采用的交叉操作，主要包括离散交叉和算术交叉

• 部分离散交叉：先在两个父代个体的编码向量中随机选择一部分分量，然后对这部分分量进行交换，生成子代中的两个新的个体。
• 整体交叉：对两个父代个体的编码向量中的所有分量，都以的概率进行交换，从而生成子代中的两个新的个体。

变异(Mutation)操作：对选中个体的染色体中的某些基因进行变动，以形成新的个体。遗传算法中的变异操作增加了算法的局部随机搜索能力，从而可以维持种群的多样性。

• 二进制变异：先随机地产生一个变异位，然后将该变异位置上的基因值由“0”变为“1”，或由“1”变为“0”，产生一个新的个体。
• 实值变异：用另外一个在规定范围内的随机实数去替换原变异位置上的基因值，产生一个新的个体。
  • 基于次序的变异：先随机地产生两个变异位置，然后交换这两个变异位置上的基因。

精英主义 （Elitism）

仅仅从产生的子代中选择基因去构造新的种群可能会丢失掉上一代种群中的很多信息。也就是说当利用交叉和变异产生新的一代时，我们有很大的可能把在某个中间步骤中得到的最优解丢失。

使用精英主义（Elitism）方法，在每一次产生新的一代时，我们首先把当前最优解原封不动的复制到新的一代中，其他步骤不变。这样任何时刻产生的一个最优解都可以存活到遗传算法结束。

遗传算法特点

• 自组织、自适应和自学习性—概率转移准则，非确定性规则
  • 确定进化方案后，算法将利用进化过程中得到的信息自行组织搜索；基于自然的选择策略，优胜劣汰；
  • 遗传算法很快就能找到良好的解，即使是在很复杂的解空间中
    • 采用随机方法进行最优解搜索，选择体现了向最优解迫近
    • 交叉体现了最优解的产生，变异体现了全局最优解的复盖
• 本质并行性—群体搜索
  • 算法本身非常适合大规模并行，各种群分别独立进化，不需要相互间交换信息
  • 可以同时搜索解空间的多个区域并相互间交流信息，使得演化计算能以较少的计算获得较大的收益。
• 不需要其他知识，只需要影响搜索方向的目标函数和相应的适应度函数
  • 对待求解问题的指标函数没有什么特殊的要求，如不要求连续性、导数存在、单峰值等假设
  • 容易形成通用算法程序
  • 遗传算法不能解决那些“大海捞针”的问题，所谓“大海捞针”问题就是没有一个确切的适应度函数表征个体好坏的问题，遗传算法对这类问题无法找到收敛的路径。
• 理论上证明算法的收敛性很困难
• 多用于解决实际问题